Where can I edit the magic container that is left of the item selected?

Does anyone know where it appears under here?

What program is this?

Hyrule Magic, the file name is "HM (New)".

Can you provide another image? You can edit a magic jar by simply selecting the red marker. As for changing the item, that requires a specific key. The annoying part about HM is that there are hidden commands that require a full keyboard to use. You cannot move doors without a num pad for example/

I found the magic that goes inside the container, but not the container itself.

Devan2002 wrote:
Does anyone know where it appears under here?

These are the blockset values, which are loaded into GFX numbers, so you can edit which GFX number coresponds to what value.
And has nothing to do with the magic bar, obviously.

Devan2002 wrote:
I found the magic that goes inside the container, but not the container itself.

This is where the GFX for the magic bar is. Everything is here: magic filled and the frame as well, but the GFX is "wrapped" meaning you will find only one gfx small square for the corner and one for the frame, which are then loded multiple times. To make for instance a horizontal bar is a whole new level of editing (ASM +GFX), but you can still make the frame less thick. There is also the 1/2 which gets loaded ontop of it.

Puzzledude wrote:There is also the 1/2 which gets loaded ontop of it.

And where is that graphic at (via HM)?

And where is that graphic at (via HM)?

I don't think you understand how this works. You can not edit gfx with HM (well you can, but it is just dumb due to being compatible only with Pant shop pro), forget HM and take YYchr. You edit gfx with the gfx editor, not HM. And all the gfx for entire HUD (heads up display) and MENU are in the gfx-area shown in your image above.

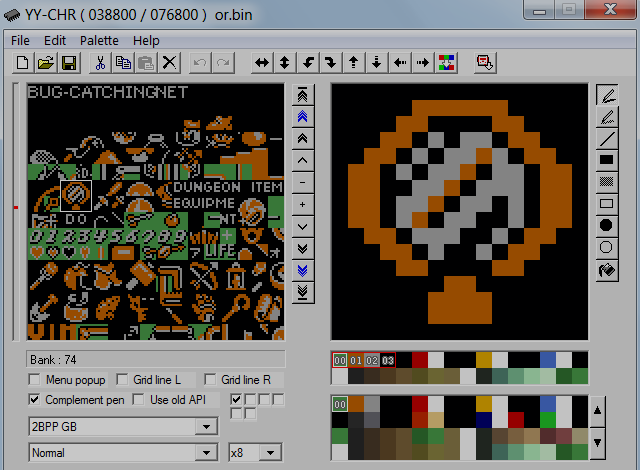
Puzzledude wrote:

What version of YY-CHR is that?

What version of YY-CHR is that?

YY-CHR ver 0.97 beta31
(c)1999-2002 Yy

I believe the one hosted on Romhacking.net is newer, but less efficient, since it is in chinese language. I'm using the older version, since it is better in my oppinion.

Do note: I also have a Palettes loaded, which originate from a ZST save state. This save state was taken on the overworld of the original game.

This tutorial here will show you how to get started with gfx editing https://lthzelda.wordpress.com/2009/06/24/lz-3-intermediate-hyrule-magic/

You'll need to use something called zcompress to properly decode the gfx files and edit them in YY CHR, the directions how to do this are all there along with links to software and other resources.

(Also, just fyi any questions like this can be posted in the Requests section, you'll find tons of info on LttP editing there)